9592. Конкатенация
двух палиндромов
Найдите
количество способов, которыми можно построить строку длины n используя k латинских
букв (размер алфавита равен k) в
виде конкатенации двух непустых палиндромов.
Вход. Два натуральных числа n и k
(1 ≤ n ≤ 105, 1
≤ k ≤ 26).
Выход. Выведите количество способов
построить заданную строку. Ответ вывести по модулю 109 + 7.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 1 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 2 |
8 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
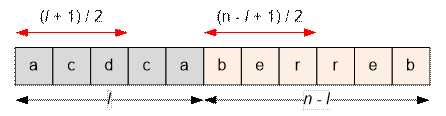
Представим
строку длины n в виде конкатенации
двух непустых палиндромов длин l и n – l.
В палиндроме длины l первые (l + 1) / 2 букв можно выбрать
произвольным образом (любую из k
имеющихся), а остальные буквы следует выбрать так чтобы получить палиндром. Это
можно совершить k(l+1)/2 способами.
Аналогично
в палиндроме длины n – l первые (n – l + 1) / 2 букв можно
выбрать произвольным образом, а из остальных следует образовать палиндром. Что
можно совершить k(n-l+1)/2
способами.
Построить конкатенацию двух
палиндромов с длинами l и n – l можно
k(l+1)/2 * k(n-l+1)/2
способами. Поскольку ни один из
палиндромов не должен быть пустым, то 1 ≤ l ≤ n – 1. Общее количество возможных
палиндромов равно
Все операции следует проводить по
модулю 109 + 7.
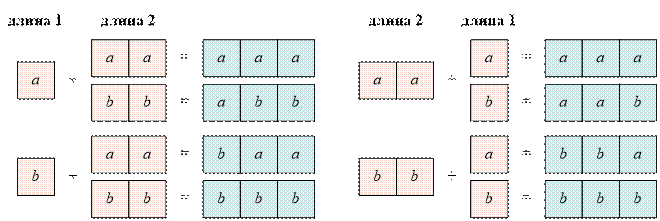
Реализация алгоритма
Вычисления проводятся по модулю 109 + 7.
Определим модуль MOD.
#define MOD
1000000007
Функция powmod вычисляет
значение xn mod m.
long long
powmod(long long x, long long n, long long m)
{
if (n ==
0) return 1;
if (n % 2
== 0) return powmod((x * x) % m, n / 2,
m);
return (x *
powmod(x, n - 1, m)) % m;
}
Основная часть программы. Читаем входные данные.
scanf("%d %d",
&n, &k);
Вычисляем ответ res по
формуле.
res = 0;
for (l = 1; l < n; l++)
res =
(res + powmod(k, (l + 1) / 2, MOD) *
powmod(k, (n - l
+ 1) / 2, MOD)) % MOD;
Выводим ответ.
printf("%lld\n",
res);
Java реализация
import java.util.*;
public class Main
{
public final static long MOD = 1000000007;
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long k = con.nextLong();
long res = 0;
for (long l = 1; l < n; l++)
res = (res + PowMod(k, (l + 1) / 2, MOD) *
PowMod(k, (n - l + 1) / 2, MOD)) % MOD;
System.out.println(res);
con.close();
}
}
Python реализация
Вычисления проводятся по модулю 109 + 7.
Определим модуль mod.
mod = 10 ** 9 + 7
Читаем входные
данные.
n, k = map(int, input().split())
Вычисляем ответ res по формуле.
res = 0;
for l in range(1,n):
res = (res + pow(k, (l + 1) // 2, mod)
*
pow(k, (n - l + 1) // 2, mod)) % mod;
Выводим ответ.
print(res)